by Lere O. Shakunle,
The Matran School of Mathematics,
Berlin, Germany.
ABSTRACT
OSD is concerned with [the construction of] organs which begin as mind simulators - with "mind" based on the Theory of Mind in "Principles of Transfigural Mathematics"[1] in the chapter, "Identity" - and from there graduate into minds of their own. At the base of OSD are questions which design engineers in particular and construction engineers in general don't like. Do OSD organisms evolve or are they the products of spontaneous creation? What is the nature and the stuff of their minds? Indeed what is "mind" in OSD? How do these organisms which have some human and machine capabilities unify individuality - a human characteristic - and collectivity - the central quality of particles which are at the basis of the materialistic outlook which props the mind=machine equation? What technology do we get where our theory of mind is such that can take us closer to the identity self than the other conventional theories? These are some of the questions which could be addressed to the subject-matter of this paper, Itsons. Itsons are not atoms. Based on what the model presented in this paper an itson is the indivisible unit of cognition.
Generally itson is an indivisible unit of thought. Thought we define as the carrier of The Idea which is the seat of Identity. That is, the nucleus of The Idea is Identity. The Idea is a spectrum. This spectrum is composed of ideas. An idea is the carrier of the reality of a thing. That is, what a thing is, is contained in the idea of it. An idea, as we know, is indivisible. Every idea is a whole thing. An idea of a thing is indivisible from the space - or time - of the thing. And since space and time are also ideas, this means that a thing, its space and time are an indivisible unified whole. This is the metaphysics of the unified space outlook[2] in which the itsons find their being. Itson rolls space on itself like an envelope. Indeed the presence of itson rolls space like bringing the ends of a wrapper together.
Geometrically , in the philosophy of space called unified space outlook, behaves as folds. Itson transforms space which also transforms it. What we get in the end is unified space in which the dichotomy of field and particle has no place. In a unified space, time is not one-dimensional. Since space folds, this means it can fold from the future to the past and so, time behaves as space in a unified space. Unified space is deeper in its epistemological implications than the curved space since all the phenomena in curved space are possible in folding space while most of the phenomena in folding space are not possible in curved space. Folding space can be used to explain not only physical events but also psychical experiences. Itsons, which are contained in the three domains of a zero spiral[3], are hooked to one another in the webloids of webs. This makes it possible for them to behave as individuals and as collections. As we shall see, a single itson is enough to make a world that ticks like ours. By stretching our metaphor beyond the creative potential of a single itson, to make our world beautiful we need two itsons and for unity in diversity we need three itsons. OSD as a post-machine age engineering paradigm unifies fundamental research and applications.
-- Lere O. Shakunle, Berlin, June 1996
0.0 Introduction
This paper begins in a terrain that the engineers don't like. Engineers don't like philosophical matters even when coined in the language of the levers of Archimedes, the first formalized mechanical device. And so when you speak of a new philosophy of engineering you can hope to get a hearing from engineers if you quickly add "and its relation to logic of machines machine design and automata concepts". I can understand the impatience of engineers with philosophy. What I fear is the danger of this impatience to our lives. For example, I have always wondered why it is not possible to get a machine architecture that can harmonize with Nature. I see the disruption of harmony as I leave the greens of the countryside for the hurly-burly of the city. What contrast! I see that if Nature is music, the architecture of the houses looks like a pandemonium let loose by the jeering hum of bees. Excuse me, I am not trying to play down the wonders of our architecture. I love some of the products of this architecture and respect the thoughts that go into them. My problem is the peace and the quietude radiated by the architecture of Nature depicted in the logical shape of the tree, the balming caress of the passing wind, indeed in the harmonious juxtaposition of things for which, up to now, we have no answer. Yet the paradox of it: the geometries of some of our architecture are superb and a few remain a challenge to the geometrical feat of Nature witness the many-dimensional architecture[4] of the hyperspace. This problem originates from lack of unity of the inner and the outer hemispheres of awareness that leads to dichotomy between mind and its creations, between Mind and Nature and between Nature and the Being. The effect of this dichotomy is the split of consciousness that leads to two worlds with no sands of comprise between them. This gulf à la dichotomy, indeed the state of a house divided against itself, epitomized by Cartesian dualism which finds its translation in the Yes-(or)-No dichotomy of binary logic which is at the basis of digital technology, leaves its stamp in all of our creations. I am sure all this is taxing the patience of an engineer who would like to begin a journey where it begins without the history of it, without the promise of it and maybe without asking the need for the journey at all. Now a promise. The next sentence takes us into the issues which this paper sets out to address.
Can there be a new paradigm in machine design without a new over-arching paradigm of engineering? Let's replace some words and see what we get. Can there be a new paradigm in mechanics without a new all-encompassing paradigm in physics? If we say yes, this will mean changing a system from within. If we can do this, then we can expect the ripples of a change generated from within spreading out until they reach the fringe of the entire system. So all you need to change the whole of physics is to change a part of it, say its mechanics. And so, by the same token, to change the whole of engineering all you need do is change a part of it which in this case may be the logic of machines and from their change the logic of their design and from there change the concepts and so doing, build new foundations of engineering.
This is one of the things I intend to accomplish in the two parts of this paper.
1.0 Mind Makes, Nature Realizes
That the Mind makes and Nature realizes savors of intrinsic cooperation between Mind and Nature. It sounds as if Nature can realize whatever the Mind creates. I use capital "M" for "Mind" to create the impression of our having solved the puzzle of what the mind is while I use capital "N" for nature so we cannot confuse Nature with the 'nature' of things which, though a property of Nature does not exhaust it. When I say "Mind Makes, Nature Realizes" I mean then that we expect Nature to cooperate in the realization of the creations of the mind. This is not always the case. However, I have come to see that if a mathematics and its arts are deep enough, Nature can take care of the sciences of any creation of the mind however involved. And as history has taught, there can be no speculation in science because any science that is worth its name needs a language. This language is encoded in its mathematics.
Anybody who has cared to look behind the graphs of experimental physics would have had occasion to ask whether it is not possible for a child to scratch on the paper and ask Nature to realize it. Children do these things on the paper everyday around the world. I have come to see that Nature can only cooperate with the child if s(he) can explain what the scratches mean. To do this, the child must show that the scratches have some patterns. These patterns are then the carriers of definite information. Indeed these patterns encode some information which Nature can only decode. This is the realization part of the patterns by Nature. As adults we know that we begin to take interest in the scratches of children the moment these scratches begin to take on some form. This is a crucial formative period for children. This period announces their minds being at work at last. Nature does not demand less of the creations of the Mind. Even though they are beyond what the common sense can grasp which is the case with most of the creations of the mind, they must be written in a language that is free. Mathematics is the key to absolute freedom[5].
And so, those lines on the graph paper for experimental physics, I got to know after doing my own thinking on this and other matters, must, for Nature to cooperate in their realization, have some structure in which some patterns are embedded. What we get in the end is that Nature can only realize what the Mind makes if it is founded on a mathematics.
2.0 Machines, Individuality and Foresight
Machines, like atoms, lack individuality. We can reproduce every computer, every integrated circuit while billions of electrons are the same as billions of sausage machines. The corpusculian philosophy attempts to individuate the atom, a model which finds its translation in differential calculus. The identity of the pointmass is in this case taken care of by the parameters of space and time[6]. This atom is here and now and its place is secured by its presence. This logic of identity breaks down where we take a peep into the constitution of the atom. The same metaphysics which gives us the corpuscle gives us a relational philosophy of space on which the Newtonian mechanics is based. In this relational scheme[7], a thing is not the same as the space it occupies.
Space is therefore the container of the atom or particle or pointmass. If the particle is not the same as the space in which it is embedded and if its identity is determined by the space it occupies, we can then ask to know what is left to talk about of the identity of a pointmass. For a thing to be defined in terms of another requires that they are connected. Since in the corpusculian metaphysics, the pointmass is not the same as the space it occupies, this means space cannot be used to define its identity. If anything space can be used to define its particularity. And, as we know, there is a world of difference between identity of things and their particularities. If space does not play internally any role in the internal structure of a pointmass other than a harbor, we can therefore not use this as a parameter in the definition of its identity.
What options are left for us if we still decide to use space and time as constituents of the identity of particles? We can say whatever identity an atom has is determined by its being in space and time in the substantial outlook[8]. While this is enough to make a mechanic it is not enough to explain the life of an organism. And so, the atomic outlook breaks down in a world where organisms derive their identities from their lifelines which are internal to them and whose projection we see as their externalities. All this shows that there is a fundamental contradiction in the atomic outlook. The internal constitution of electron says that every electron is like every other electron. This structure of an electron or pointmass does not meet the basic criterion of identity which is uniqueness. If we then say that space and time give a pointmass its identity then if space is not the same as the pointmass then we cannot use space to confer identity on a thing that does not belong to it. What we get under such a scheme is not an atom with identity but identical atoms with particularities.
I am sure somebody is growing impatient with all this. This person is an engineer. He would like to know what all this has to do with machine design and the talk of a post-machine engineering paradigm. I hasten to say everything. And this is what I intend to show in what follows.
3.0 Structure of Itsons
Before we get into the structure of itson, first the features. Even before then, a general remark.
A General Remark:
Three of the fundamental features of Itsons are:
From this follows
Aii. Itsons is the common language of Mind, Nature and Being
Two of the special features derived from the above fundamental features are:
Bi. No two itsons are the same
Bii. Every itson is an indivisible unit of thought which is the carrier of idea and the seat of identity. Identity is in part cognitive-molecular by which we mean part of identity is cognitive-genetic.
-- The itsons of this paper are based on this interpretation
Structure of the Itson:
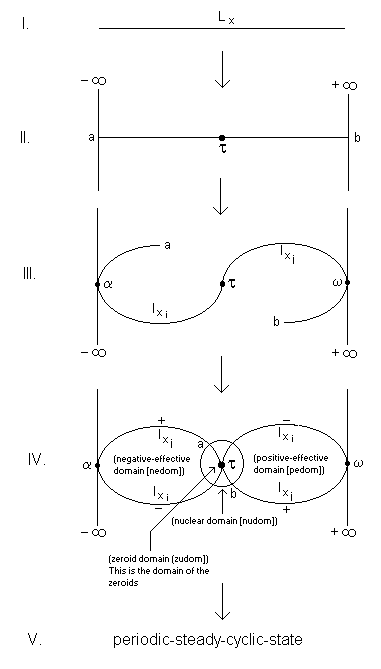
Geometrically itson is the indivisible unit of a lifeline. Lifelines are potential curves at every point. A lifeline line bends into a curve which grows into a fold at infinity. Every point on the lifeline is a curve. Every curve is a potential fold. Both sides of a point are minus and plus domains whose summation is an inexhaustible zero. The minus and plus depict positive and negative infinities whose addition is the absolute zero. This means every point on the line is the summation of infinities. There are three types of infinity in a lifeline. These are
(ii) outer infinity,
(iii) absolute infinity.
Point in a lifeline unifies the features of points in Euclidean and non-Euclidean geometries. The life history of a lifeline is concentrated on the point.
In what follows we shall present the itrons of a muson. Don't try to figure out what an itron or a muson is. The geometry of the lifeline that follows shall help fire the imagination to the extent that by the time we get to the end of this first step in its introduction we can be able to say that we have some idea of what an itson is and how it relates to the muson which is the local domain that harbors it.
As our first step in the introduction of this geometry, we shall explore together three axioms of the line of spiral geometry. Even though we have said it before we hasten to repeat that when we talk of the line in spiral geometry which is the geometry of the physics of infinity one of whose organs are the itrons, we mean the "lifeline".
4.0 Axioms of the Line
Axiom I:
Every straight line is a curve at infinity.
For this we have
Like we said, there are three types of infinities in the lifeline of spiral geometry.
[ In the text of this document, we shall use the characters o-o to represent the symbol for "infinity" and the text /a, /t, /z and /w to represent the subscripted Greek mathematical symbols -Ed.]
These are:
To extend it you need to get away from it all. This we can liken to a ship disappearing from your gaze. The point at which you can no longer pursue a thought because it is becoming a downpour or thinning out is the place where infinity is placed on the line. In the case of a ship disappearing, it is the point where the line that connects you to the ship bends and comes back to you thus making you the center of the line. One of the peculiar features of this lifeline is that all you need to is put a point on the paper, move it to the right and you get same length of the line on the left. Thus every point on the life line produces lines on both sides of it such that the point - any point at all - is always at the center of the lifeline. In the case of an idea whose thought requires a pause either to maintain your sanity or for a new input, the point of infinity is where you take the pause and go back to another state which has nothing to do with the idea. This time the line returns to the possessor of the idea who is, in this case, the center of the lifeline.
In [Fig. IV] something strange seems to be happening. There is symmetry in what is presented but internally things are asymmetric. We would not say whether this is in the short or long run. What we have is that in the alpha domain on the left, even though the lines that go out and return to the point are positive and negative, because the alpha region is a negative region, the negative is more effective than positive in this domain. The same holds for the omega domain on the right. This is a positive region and so even the lines that go out and come back are effective in the positive. If we want to use this as a cosmological model called periodic-steady-cyclic-state (PSCS)[9] we are faced with some tough questions. Some of the questions are:
ii) how does the negative effectiveness relate to the positive effectiveness?
iii) what is the nature of the connection of these domains in the nuclear domain, and
iv) what role does the nuclear domain in the effectiveness of the domains?
One thing we know for sure and that is the effectiveness of the domains are cyclic. These cycles are conditioned by periods. Thus there are cycles which are steady for a period and non-steady in another period. The whole structure tries at all times to maintain its equilibrium. Thus is the negative effectiveness of the cycle is more than its positive effectiveness we can expect that before the system crashes under this imbalance the next cycle swings in with more positive effectiveness. These is something strange about how this cosmic balance is kept. These matters are tackled in spiral geometry and in The Folding Universe[10].
Axiom 2:
A curve is the extension of the line
This has been demonstrated in the figures above. We see that the line under the arrow is longer than the one from which it originated which is the line above the arrow. This means a line extends as a curve. We do not say that "a line extends in 'becoming' a curve" because the word 'becoming' gives the impression of evolution. In the transformation of a line into a curve at infinity there is nothing evolutionary about all this since the lifeline is intrinsically a curve. What the infinity does is make explicit the implicit property of the lifeline.
Axiom 3:
The center is everywhere on the line
For this we also have
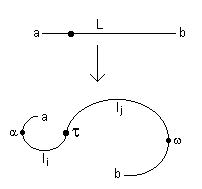Both a and w are the local domains of the nuclear domain /t. That this
is so is what we tried to show above. Given a physical line, the point in the
above figures is not at the center of the line. In a lifeline, any point,
wherever it may be, is the center of the line. In a lifeline a center is
determined by the /a and /w on both sides of it while itself is /t. Every
point on the lifeline has these qualities. Another implication of this
axiom is that the line is discrete as it is continuous. Discrete because
there is the point everywhere on it and continuous because these points
are connected without gaps. If we can get inside the line we can
see the arrangement of these points but because we cannot get inside
it, what we see is a line.
Axiom 4 :
Every curve is a potential curl
This gives
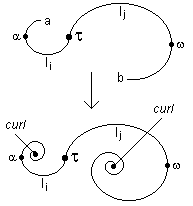
Axiom 5:
A curve with an implicit center is a fold.
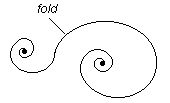
The superimposition of two folds of itson gives
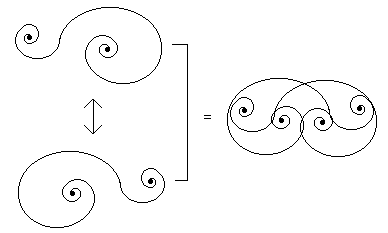
Two folds of itson give a fold of one of the zero spirals below:
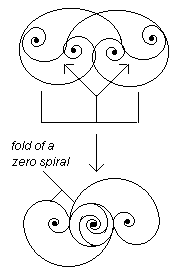
The two points in the middle of the two folds above the arrow collapse into a single point in a zero spiral. These two points merge inside the central point of the zero spiral. In the fold of the zero spiral we also have the negative-effective a-domain of the musons, the positive-effective w-domain of the plusons and nuclear t-domain whose core is the zeroid of the trasons. The superimposition of the folds of itson, as we have seen, makes a single fold of a zero spiral. As of now there are three types of zero spirals. The folds of this work shall be confined to only one of them. Suffice to say that the primary building block of this zero spiral are the sinuroids which are the special curves of a fold.
Fundamentally the fold above is a line. According to Axiom 3 which says that the center is everywhere on the line, we see that the lines is made of points which have a common thread running through them. This common thread of unity is what makes the points a line. For a deeper grasp of the ontological ramifications of the common thread of unity the reader is referred to the logic numbers[11].
These axioms lead the way to the itsons.
The special features of itsons are:
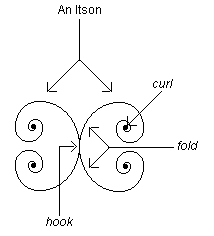
The most mysterious aspect of an itson are its curls. The problem is that itsons curl inward and spread outward. This means the curls belong to the region of inner infinities. We can surmise that they are folds which may not be the same as the folds of the itsons depicted below. But if they are folds, this would then mean they end up again as curls! As of now, every model of a curl is a paradox box. One has tried to use the quarks as analogy. It didn't work. The reason for this is obvious. Our itson is the smallest unit of cognition. The curls are the endpoints of the fold. The curls point inward and not outward therefore they are a kind of inner dimensions.
Before we go to the engineering aspects of itsons as these relate to composing and encrypting of information, we hasten to have a look at a muson with its itsons:
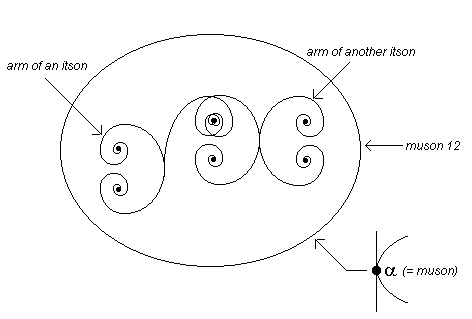
We showed above two itsons of muson [12]. In actual fact, we never can tell how many itsons make a muson or a pluson. What we present above is used to show how itsons and musons relate.
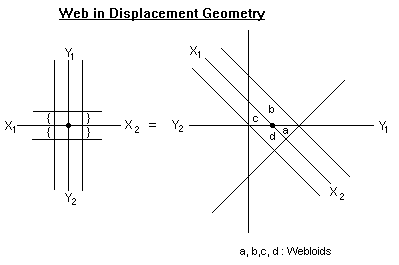
5.0 Webs and Webloids
Have you ever watched a spider at work while constructing its web? With so much distraction of the city, the romance of the countryside is becoming the sole possession of poets. I used to have this opportunity and made the most of it as the school garden.
The school garden is the domicile of pupils in those days whose punishment deserved more than the cudgel. You are sent to the school garden to till the soil a whole day for missing the singing or the sports. You don't like this work at all. You love the garden since you don't need to bother for your meal for the day. The garden has a surplus of the fresh and the juicy to adorn your make shift table on the ground. Really you do have your breaks in between at which time you can look around. If you look around enough and can allow your gaze the freedom to take you where it will, surely it will take you to the spider under the orange tree. There! Under one of the branches you could see a spider busy constructing its web. Sometimes it looks as if it will fall off and before you shout, "Don't", off it goes to another branch only to perch there, dangling dangerously inside one of the segments of its web. This segment which can be likened to a room in house (that is the web) I call the webloid.
A spider's web is an excursion is the beauty of topology. The lines are sometimes collapsing; they wobble at some places without the loss of their intrinsic unity. If you want to get away from the oppression of your tilling in the school garden, you can just hold up a stick and let go on a line of the webloid of the web complex. The whole edifice looks like crashing down.
It doesn't. And this is where you begin to see one of the wonders of the geometry of the architecture of the spider's web: the disturbed webloid joins the line of another webloid and before your hurrah translates into the hilarity a broad smile, a new web has emerged.
Itsons are embedded in webs. The webs and their webloids 12 of this work shall challenge the architectural wonder of a spider's web. They are not webs built on impressionism otherwise we would have copied the spider's work. If anything cubism can provide a gateway to the webs of itsons. This means dismantling the web of a spider and reconstructing it by changing the positions of the webloids. However, what we really want to do is challenge geometric creativity to give us a web that can make a spider learn from us.
The webs in which itsons are embedded are, based on the unified space outlook, indivisible from itson. This means, in this case, the web with its webloid is part of the structure of itsons.
6.0 Itsonal Scripts
An itsonal script is an information composer.
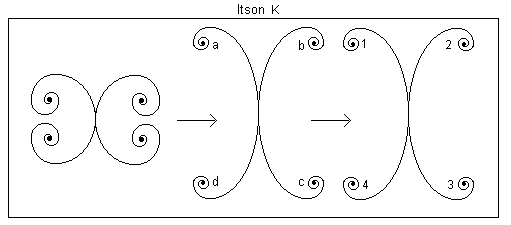
From what we have come to know about itson, we can now wade into the composition of itsons which is at the basis of the processing of information. In the example that follows we want to show the first step in computational itson. One of the algebras of itsonal computation is presented below based on Itson K. Before this algebra we would like to show how a single itson can populate the whole world. In the beginning was itson K below:
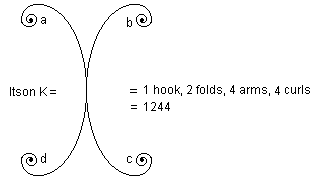
for which we have the table
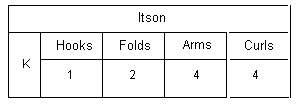
We can translate all this into a function where f represents an itson and what is in the brackets after f the itson in question. Thus f(K) will then mean "itson K". Therefore for the table above we have f(K) = 1244. We hasten to say that the numbers assigned the curls are matters of choice. What we should not forget is that we are dealing here with the simplest itson. Really, the numbers of itsons are based on logic numbers which are metaphorically richer than classical numbers. In this paper which sets out to introduce the itsons, we present them "as if" we can reach them with natural numbers.
What happens is that an itson separates at the hooks into folds. For Itson K we therefore have
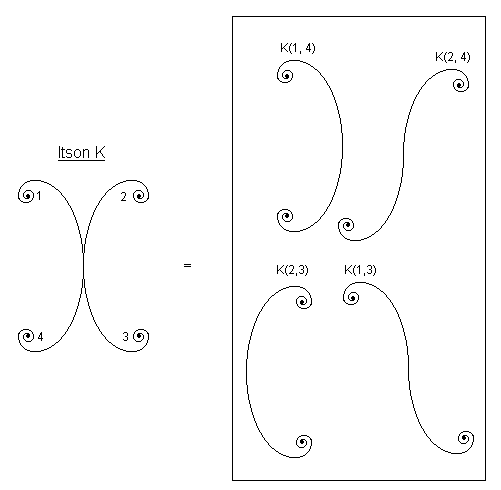
We cannot say for sure how many hooks, folds, arms and curls will emerge by performing the operations of itsons on the folds above.
Some of the operations of itsons are:
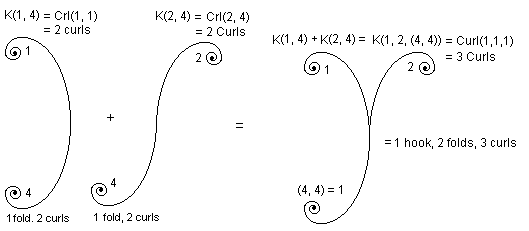
which we call Itson Ki for which we have on the left, together with arms
7.0 Computational Basis of Itsons
What we presented above is the first step in a long journey as far as the computational aspects of itsons are concerned. Generally, every itson has some linear and non-linear aspects. For the second step we need the webs. In this case we take a complementary web.
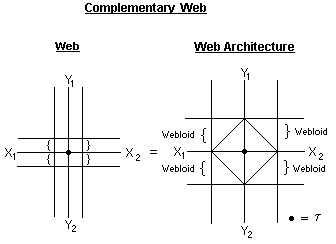
Generally an itson grows from within, that is, from its curls. An itson in the type of web above cannot grow. The reason is that a curl grows in contact with the line. In this case the curl can grow at both sides of X and Y. And here comes the rub. The lines of the web presented above are called the latent lines of growth of the curl. There are also potential lines of growth of the curl which we never can know. For who can say how a child or a flower will grow! What interests us is the contribution of the latent to the potential lines of growth of a curl. We need the potential lines - the non-linear aspects of itsons - to predict the growth of a curl. That we can do this does not mean we can know what will happen to the curl when the eddies it sends our return to it. This is why itsons are poetic entities per se.
Since a curl grows - by which we mean 'produces other curls' - in contact with the line, we should expect the webloids to be dense. This is exactly the case. A webloid is dense with lines. These lines are called grids. Still on a complementary web, we have below one with grids:
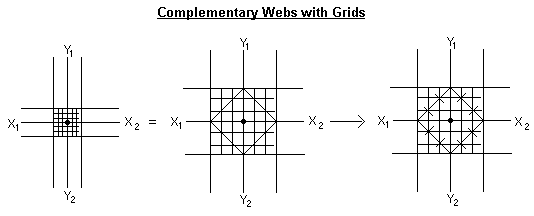
The places where the lines are crossed are points of growth on the grid. With what we know of the lifeline we would say that even the grids can be so dense to the extent that points are like beads on the line.
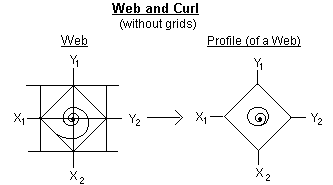
In the computational itsons, we need the web and the curls to start with. Based on the unified space structure, the webs and the curls of itsons form an indivisible whole.
8.0 Web and Displacement Geometry
A spider's web can be disturbed by fiddling with a line in a webloid. What we get is not what happens to line in projective geometry but something fundamentally different. This phenomenon led to the creation of a new geometry as part of spiral geometry by the author. I call it displacement geometry[12].
Displacement geometry is a state of chaos leaving behind an order. In this state, something is disorganized but in the end looks orderly all the same.
Imagine a wind blowing off a hut. The whole thing collapses. But the wonder of it! There is an opening where people can get into the hut. The roof is wobbled but still intact. You cannot stand up inside this hut but you can spread-eagle and sleep with ease. The plates are thrown about but none is broken. The table is overturned but you can still put some places on the platform between the legs. This is displacement geometry at work. Let's see what we get from the displacement geometry of our web.
Now what happens to a curl - or to anything for that matter - in displacement geometry? This is a question whose answer we leave for another day. Suffice to say that spiral geometry is composed of the following geometries:
ii) displacement geometry (the example above represents what we can call a foretaste)
iii) morpholinic geometry (does not feature in this paper; its original foundations already built in another Transfigural Math publication)
The curl that we have come to know is the curl we see from afar. As we get closer to the curl some of its hidden details appear. For example we begin to see that the curls are numbered - numbered in the sense that each crossing of the line is a code - like what we have below:
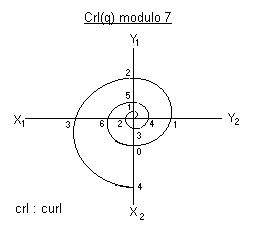
The computational relevance of this numbering shall be shown in the second and concluding part of this paper. Even as we get still closer we discover that what we have above is a profile of the curl while the real curl without the grids is what we have below:
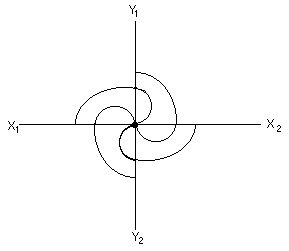
For a distant curl embedded in a web without the grids we have the fold below:
Be all this as it may we still need another step to computational itsons. This we shall present in the second and last part of this paper. The three steps are needed for computation. We hasten to say that this computation involves algebra and geometry combined, transforms which enable us to treat curves as lines, internal and external coding. There are some features that challenge mathematical creativity. One of them are the eddies of itsons. The bubbles which are the local store of energy that incorporates decision modules we can handle with ease and things remain easy-going until we reach the eddies. The physics of eddies - not to talk of the fact that as of now one does not know what is happening when a curl unfolds, spreads, and like a tide lashing at the rock at the shores, empties at the far reaches of the land as eddies with local bubbles dotting the waters everywhere - is very complicated. Generally, the physics of itsons is interdisciplinary!
9.0 Post-Machine Age Paradigm
The purpose of this paper has been to introduce the structure of itsons with minimal formalism. Really what we have done in this first part is show that it is not possible to formalize the itsons without their geometries or without the geometries that they are. Unlike what obtains in the conventional setting where one creates a science and looks round for the appropriate mathematics, itsons make it possible to talk of mathematics as that science, or that art or that engineering.
Itsons are a high-level language entities. Among other things, they set out to announce the arrival of post-machine age engineering. Unlike the machine-age paradigm which requires input of energy from an external source, an itson is the generator of its own energy. And so the question of shortage of energy does not arise since it does not need to exploit Nature for its expression. Based on the unified space outlook, the itsonal world is an indivisible unit. And so, in this arrangement, Nature is not a world out there. The itson is embedded in it like it is embedded in the web!. Itson derives its name from one of its fundamental qualities: motion at rest. This means itson is forever active. Itson means "it's on" written as "it(')son" and pronounced as "its ("o" like in "on", "n" line in "own"). Every itson generates its own internal energy. Being connected points on the lines, every itson can enlarge its own internal resources by information exchange with other itsons. However, fundamentally, every itson is self-sufficient, yet interdependent. Here we have a case of a lot being in a name!
Itsons are endowed with creative potential. This is one of the reasons why it is not possible to pin them down to a single definition. Though poetic, itsons are geometries. An itson is not a field. It is not a particle either. Its bubbles are points of concentrated energy. It reaches other itsons with its eddies. The hook of an itson is the glue of its folds.
As geometric entities enveloped in poetic romance that find their expressions in mathematics, the sciences, literature, arts and other spheres of human awareness, itsons transform themselves by their inner resources.
The second and concluding part of this paper shall be based on the algebras of the model of itsons presented in this paper. In the second part we shall show the methods of information transfer within and between itsons, modality of growth, and on top if it all, the relevance of the itsons for natural science in particular and interdisciplinary knowledge in general.
REFERENCES
© Copyright 1996. Shakunle, Lere O. All rights reserved. Reproduced exclusively
in the Journal of American Computer Science by permission of Lere O. Shakunle.
E-Mail? Send E-Mail to ACSA [ click here]
at 72662.1332@compuserve.com.